符号执行 (Symbolic Execution) 与约束求解 (Constraint Solving)

关于作者

张帅，网络从业人员，公众号：Flowlet

个人博客：https://flowlet.net/

序言

笔者最近在做通过符号执行（Symbolic Execution）与约束求解器（Constraint Solver）来自动生成 P4 程序的测试用例，符号执行是一种重要的形式化验证（Formal Verification）方法和软件分析技术。

根据软件测试 7 项基本原则中的第一条：Testing can show that defects are present, but cannot prove that there are no defects（测试只能证明软件有 Bug，但不能证明软件没 Bug），因此有必要针对软件程序通过形式验证（Formal Verification）的方式（即通过数学方法）来严格的证明系统没 Bug。

本文为软件分析学科中符号执行（Symbolic Execution）与约束求解（Constraint Solving）子系统的概念论述。

1. 符号执行

前言

符号执行作为一种重要的形式化方法和软件分析技术，采用抽象符号代替程序变量，程序计算的输出被表示为输入符号值的函数，根据程序的语义，遍历程序的执行空间。其在软件测试和程序验证中发挥着重要作用，并可以应用于程序漏洞和脆弱性的检测中。

符号执行经过了传统符号执行 → 动态符号执行 → 选择性符号执行的发展过程，动态符号执行包括混合测试和执行生成测试两种。

1.1 经典符号执行

经典符号执行的核心思想是通过使用符号值来代替具体值作为程序输入，并用符号表达式来表示与符号值相关的程序变量的值。在遇到程序分支指令时，程序的执行也相应地搜索每个分支，分支条件被加入到符号执行保存的程序状态 π 中，π 表示当前路径的约束条件。在收集了路径约束条件之后，使用约束求解器来验证约束的可解性，以确定该路径是否可达。若该路径约束可解，则说明该路径是可达的；反之，则说明该路径不可达，结束对该路径的分析。

以图１中的示例代码为例来阐述符号执行的原理，程序第９行存在错误，我们的目标是要找到合适的测试用例来触发该错误。若使用随机生成测试用例对程序实行具体测试的方法，对于整型输入变量 x,y,z 而言，其取值分别有 2³² 种，通过随机生成 x,y,z 取值作为程序测试的输入，则能够触发程序错误的可能性较小。而符号执行的处理是，使用符号值代替具体值，在符号执行的过程中，符号执行引擎始终保持一个状态信息，这个状态信息表示为 (pc,π,σ)，其中：

１) pc 指向需要处理的下一条程序语句，其可以是赋值语句、条件分支语句或者是跳转语句。２) π 代指路径约束信息，表示为执行到程序特定语句需要经过的条件分支，以及各分支处关于符号值 α_i 的表达式。在分析的过程中，将其初始定义为 π＝true。３) σ 表示与程序变量相关的符号值集，包括含有具体值和符号值 αⁱ 的表达式。

符号执行算法具体如算法１所示。

首先，由于 x,y,z 是程序的输入，将 x,y,z 的值定义为符号变量 σ:α,β,γ，且由于还未执行到任何的条件分支，因此初始状态为 σ:{x→α,y→β,z→γ}；π＝true。

这里需要说明，除去初始被定义为符号变量的 x,y,z 之外，假如在代码运行过程中出现了与 x,y,z 相关的赋值操作，则也须将新产生的变量当成符号变量进行处理。例如：假设在第２行和第３行代码之间添加一个赋值操作，即令 w=２∗x，则对应的 w 也会被认为是符号变量，因此程序状态将变为 σ:{x→α,y→β,z→γ,w→２∗α}；π＝true。

当程序分析到第一个分支判断语句 if x＞０时，将会分叉出两条路径，即 true 路径和 false 路径，从该分支处延伸出两个分析状态，分别是 if x＞0 → σ:{x→α,y→β,z→γ}；π:α＞０和 if x≤0 → {x→α,y→β,z→γ}；π:α≤０。s

首先，沿着 true 路径继续搜索，即满足 x＞０，将遇到第二个分支判断 if y＜５，从该分支处将再产生两条路径，路径状态分别为 if y＜５→σ:{x→α,y→β,z→γ}；π:α＞０∩ β＜５和 if y≥５→σ:{x→α,y→β,z→γ}；π:α≤０∩β≥５，记录 false 的路径状态；继续沿 true 路径搜索，遇到第三个分支判断 if y＋z＞０，产生两条路径及两个新的状态 if y＋z＞０→σ:{x→α,y→β,z→γ}；π:{α＞０∩ β＜５ ∩ y＋z＞０} 和 if y＋z≤０→σ:{x→α,y→β,z→γ}；π:{α＞０ ∩ β ＜５ ∩ y＋z≤０}。

至此，与符号变量相关的操作都已处理完毕，则需要使用 SMT solver 来求解满足各路径约束条件的解，求解得到的解即为沿该路径执行的测试用例。例如，最终执行到 if y＋z＞０的路径的解需满足:α＞０ ∩ β＜５ ∩ y＋z＞０，得到的解之一可能是 α＝１,β＝２,γ＝１，该测试用例执行程序得到的结果为 a＝－２,b＝１,c＝２，执行完该路径后，符号执行继续沿 false 路径 if y＋z≤０进行求解测试，约束条件为 α＞０ ∩ β＜５ ∩ y＋z≤０，得到的解可能是 α＝１,β＝２,γ＝－３，得到结果为 a ＝－２,b＝０,c＝２。依次类推，执行完第三个分支的两条路径后，将从保存的状态中取出第二个分支处记录的状态，并求解生成测试用例来测试程序。

传统符号执行在原理上是可以对程序路径进行全覆盖的，而且可以针对每一路径都生成符合该路径的测试用例。

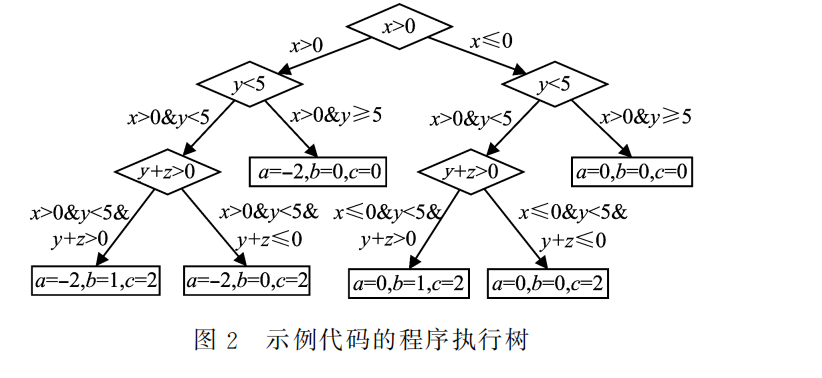示例代码的程序执行树如图２所示。

程序中有３个分支判断点，总共有６条路径，即符号执行引擎需要进行６次约束求解，并得到针对６条路径的测试用例。其中，求解约束 x≤０ ∩ y＜５ ∩ y＋z＞０得到的测试用例，执行结果为 a＝０,b＝１,c＝２，将触发程序错误。

1.2 符号执行的发展

根据发展状况，可以将符号执行分为经典符号执行、动态符号执行和选择性符号执行。经典符号执行并不真实地执行，而是基于解析程序，通过符号值模拟执行；动态符号执行结合使用了具体执行和符号执行，综合了具体执行和经典符号执行的优点，并出现了混合执行（concolic execution）和执行生成测试两种符号执行技术；选择性符号执行可以对程序员感兴趣的部分进行符号执行，其他部分使用真实值执行,代表工具为 S2E。

混合执行由 Godefroid 和 Sen 等在 2005 年提出，Sen 阐述了其原理，并总结了近十年来的改进与发展；执行生成测试是由 Cadar 等于 2006 年提出的，并在 EXE 和 KLEE 工具中得到了实现；选择性符号执行由 Chipounov 等于 2009 年提出，并在 S2E 框架中得到了实现。

1.3 混合执行

混合执行结合使用具体执行和符号执行的软件测试技术，是动态符号执行的一种。其主要思想是用具体输入执行程序，在程序运行的过程中，通过程序插桩手段收集路径约束条件，按顺序搜索程序路径，利用约束求解器求解上一执行中收集到的约束集，从而得到下一次执行的测试用例；在下一次执行结束后，按一定的策略选择其中某一分支判断点进行约束取反，得到新的约束集，再用约束求解器对其进行求解，得到下一执行的测试用例。如此反复，可以避免执行重复路径，从而以尽可能少的测试集达到高测试覆盖的目的。

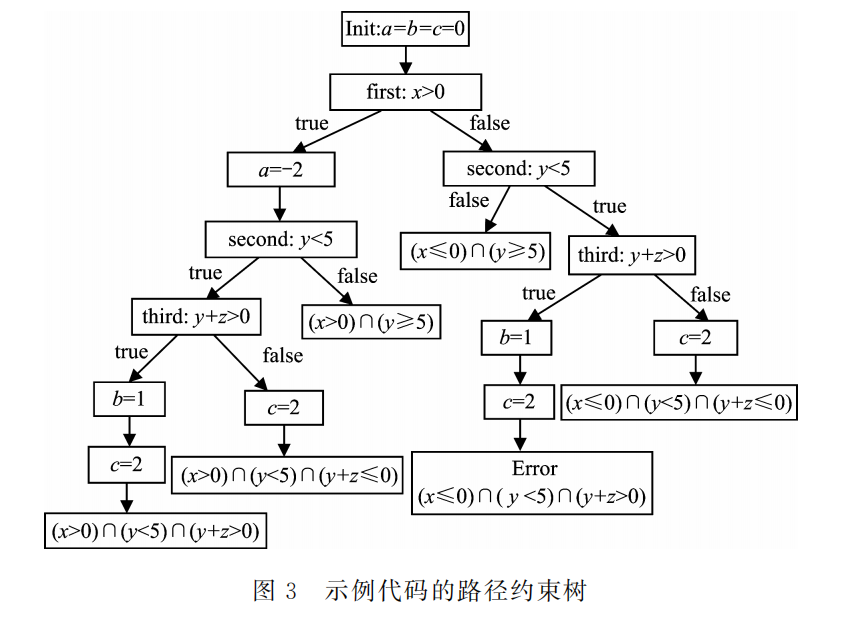
以图１中给出的示例代码为例，解释混合测试的测试流程。图３给出了该程序的路径约束树，可以看出，该程序共有６条不同的路径，对于每一条路径，都有其对应的约束集。从路径约束树可以看出，该代码有５条正常执行结束的路径和１条错误路径。通过约束集确定程序执行的轨迹，引导程序沿设定的路径执行。对于示例程序而言，能够触发程序错误的约束集为 (x≤０)&(y＜５)&(y＋z＞０)，在程序执行过程中，收集并保存该执行路径的约束。为了对该代码路径进行全覆盖，程序将被执行６次，并且每次执行都是通过选取一个约束条件进行取反后再求解出新的测试用例，以测试另一路径。

例如，选取初始测试输入设定 x＝y＝z＝１，在具体执行过程中，由于１＞０，因此将执行a＝－２；接着由于１＜５且１＋１＞０，将执行b＝１，c＝２。程序正常执行结束，在执行过程中收集该路径的约束为 (x＞０)&(y＜５)&(y＋z＞０)。为了使下一次执行能覆盖到程序的不同路径，混合测试以一定的策略选择其中的一项分支判定条件进行取反，即将上一执行中收集的约束条件取反，得到新的约束集(x＞０) ∩ (y＜５) ∩ (y＋z≤０)，通过求解该约束得到新的测试用例 x＝１,y＝１,z＝－２；用新生成的测试用例执行程序，执行过程依次为 a＝－２,c＝２，执行结果为 a＝－２,b＝１,c＝２，程序正常执行结束。

在该轮运行之后，没有出新的约束，因此约束集为 (x＞０) ∩ (y＜５) ∩ (y＋z≤０)，下一轮的约束取反将约束集变为 (x＞０) ∩ (y≥５)，求解生成新的测试用例为 x＝1，y＝５，z＝－２，程序依然正常运行结束。

依照此过程，反复进行具体执行并收集路径约束，以及约束取反生成新的测试用例的过程，在求解约束集 (x≤０) ∩ (y＜５) ∩ (y＋z＞０)，得到测试用例 x＝－１,y＝１,z＝２时，执行结果为a＝０,b＝１,c＝２，因为 a＋b＋c＝３，所以将触发程序第９行的错误。

利用混合测试验证程序的正确性，在理论上是可以对程序路径进行全覆盖的，但是随着分支的增加，程序状态空间呈指数型增长，再加上约束求解的限制，混合测试在现实软件测试中的应用还存在一些问题。例如，Rupak 等提出的 hybrid concolictesting 的核心思想是结合随机测试和混合测试方法对程序进行测试，以保证对程序状态空间搜索的广度和深度。该方法融合了混合测试详尽彻底和随机测试快速高效的优点，提高了程序测试的覆盖率。

1.4 执行生成测试

执行生成测试也是融合了具体执行与符号执行的软件测试技术，由斯坦福大学 Cristian 等提出并在 EXE 中实现。执行生成测试与混合测试最大的不同点在于将符号执行和具体执行混合的方式不同。执行生成测试的混合是在一次程序执行中，对符号变量无关的代码段使用具体执行；而对符号变量相关的代码段进行符号执行，使用符号执行引导测试过程，为每条路径生成一个测试用例，并进行一次执行。

执行生成测试的核心思想是通过程序代码自动地生成潜在的高度复杂的测试用例，在用符号输入执行程序的过程中，在分支处将 false 路径的状态信息记录下来，判断为 true 的分支继续执行。记录其约束信息，通过求解这些约束信息得到该路径的测试用例，该分析过程就是执行生成测试。

下面以图１中的示例代码为例来阐述执行生成测试的处理流程。

１) 设置初始状态：将 x,y,z 设置为符号变量，且任意取值。由于 x,y,z 的类型为整型，可以将其取值限定在 INT_MIN 和 INT_MAX 之间，因此添加约束条件：x,y,z≥ INT_MIN ∩ x,y,z≤ INT_MAX，用符号输入执行程序。

２) 在第一个条件分支即第３行处分叉执行，将 true 分支上的约束条件置为 x＞０，false 分支上的 x 约束条件为 x≤０。选择其中的 true 分支继续执行，false 分支以栈的形式克隆存储。

３) 在第二个条件分支(第４行)处分叉执行，将 true 分支上的约束设置为 x＞０ ∩ y＜５，false 分支上的 x 约束条件为 x＞０ ∩ y≥５。选择其中的 true 分支继续执行，false 分支克隆存储。

４) 在第三个条件分支(第５行)处分叉执行，将 true 分支上的约束设置为 x＞０ ∩ y＜５ ∩ y＋z＞０，将 false 分支上约束设置为：x＞０ ∩ y＜５ ∩ y＋z≤０。选择其中的 true 分支继续执行，false 分支克隆存储。

５) true 分支由于不满足第７行的约束 a＋b＋c＝３，执行到程序退出(第１０行)，求解符号约束 x＞０ ∩ y＜５ ∩ y＋z＞０，得到第一个测试用例。

６) true 分支执行结束，从克隆存储中依次取出分支记录，第一个取出的是约束条件为 x＞０ ∩ y＜５ ∩ y＋z＞０的分支，求解得到第二个测试用例。

７) 依次从克隆备份中取出分支记录，并求解得到测试用例，直到分支记录栈中为空，得到针对所有路径的测试用例。其中有一分支会执行到错误代码处(第９行)，此时的分支约束为 x≤０ ∩ y＜５ ∩ y＋z＞０，求解该约束得到触发该错误的测试用例。

与混合测试相比，执行生成测试的优势是能更加系统且高效地得到所有的路径信息以及对应的测试用例，避免重复性搜索过程；其缺点是内存空间耗费较大，一种解决思路是可以使用多线程的方式代替分支存储，实现对多个分支的同时搜索和测试用例的生成。

1.5 选择性符号执行

受路径爆炸和约束求解问题的制约，符号执行不适用于程序规模较大或逻辑复杂的情况，并且对于与外部执行环境交互较多的程序尚无很好的解决方法。选择性符号执行就是为解决这类问题而出现的符号执行分析技术，其也是具体执行和符号执行混合的一种分析技术，依据特定的分析，决定符号执行和具体执行的切换使用。在选择性符号执行中，用户可以指定一个完整系统中的任意感兴趣部分进行符号执行分析，可以是应用程序、库文件、系统内核和设备驱动程序。选择性符号执行在符号执行和具体执行间无缝地来回转换，并透明地转换符号状态和具体状态。选择性符号执行极大地提高了符号执行在实际应用中对大型软件分析测试的可用性，且不再需要对这些环境进行模拟建模。

选择性符号执行在指定区域内的符号化搜索，就是完全的符号执行，在该区域之外均使用具体执行完成。选择性符号执行的主要任务就是在分析前将大程序区分为具体执行区域和符号执行区域。这种选择性是指只对有必要的区域进行符号执行，是将实际应用系统缩放到符号执行可用规模的关键要素。

同样地，以图１中的示例代码为例来阐述选择性符号执行的原理，假设仅对代码中第４－７行的代码段进行符号分析，而对其余部分进行具体执行。选择性符号执行的核心是符号执行和具体执行的交互处理，即在具体执行转入符号执行区域及符号执行转入具体执行时的处理。

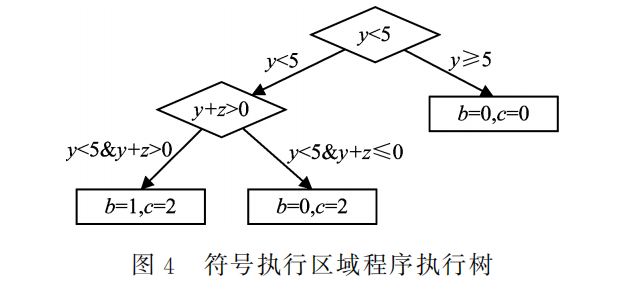
对选定的代码段进行符号分析，其符号变量仅有 y 和 z，而 x 只需作为具体值。假设随机生成的初始输入为 x＝０,y＝０,z＝０，执行程序将得到结果 a＝０,b＝０,c＝２。在代码执行到符号执行区域时，将进行０→y 和０→z 的变换，并进行符号分析。该代码区域的程序执行树如图４所示。

在该代码区域内的符号分析与全程序的符号分析过程一致，可以根据不同的约束信息求解生成不同的测试用例来对目标程序进行执行，在执行完第７行代码后，将符号变量 y 和 z 变换为具体值，即 y→０和 z→０，继续具体执行剩余代码，则本次执行完成。之后，依据符号分析的结果，随机对 x 取值，生成测试用例，如 x＝２,y＝６,z＝０，执行程序结果为 a＝－２,b＝０,c＝０，未触发程序错误，并继续生成测试用，例如 x＝－１,y＝２,z＝－３，执行程序，依据符号执行区域内的分支约束求解执行不同路径的测试用例，直到将目标符号分析区域的路径都执行完毕。由于 x 的取值始终是随机的，因此可能导致即使遍历了符号执行区域内的所有路径，最终也无法触发程序错误。唯有当符号执行区域执行到路径 y＜５ & y＋z＞０时，x 的取值刚好满足 x＜０，则会触发程序错误，即程序错误触发的情况仅以一定的概率发生。

选择性符号执行的关键挑战在于使这种将符号方式和具体方式表示的数据与执行混合，同时须兼顾到分析的正确性和高效性。因此，需要在具体区域和符号区域设置明确的界限，并且数据必须能够在执行越过所设置的区域界限时，完成符号值域具体值间的转换，这也是选择性符号执行的贡献所在：正确执行一个真实系统及其必要的状态转换任务，在一定程度上达到了最大化本地执行的目的。

2. 约束求解

前言

“约束求解”，一般是指一种方法论：强调对问题通过某种数学语言进行形式化表达，然后对其进行求解，是计算机解决问题的一种常见方法论。因此，“约束求解”是跨领域的，在形式化方法领域提到它一般想到的是可满足性问题，在运筹学领域提到它想到的是数学规划问题，在 CAD 领域提到它想到的是几何约束问题。

2.1 约束求解

约束无处不在，约束是一个现实世界普遍存在的概念。从个人生活，到工业领域，到国计民生都有体现。比如：我们制定旅行计划，受到时间和开销的约束；学校制定排课安排，受到教室资源，教师和时间等的约束；工厂加工产品受到产品加工顺序和机器资源的约束；芯片设计，受到功能需求和工艺的约束等等。

发现场景中的约束，不同视角：

事实/规则。（比如，当按钮被按下时，门就打开；一天有24小时；John 是 Alice 的老师）
必须做的。（比如，离开房间的时候必须关灯）
不能做的。（比如，不能闯红灯）

生活中我们谈“约束”可能倾向于最后一种，而容易忽略其他两种。基本上，很多问题把以上 3 个视角都考虑了，约束就找的差不多了。

在数学中，约束是一个广泛的概念，指的是数学量需要满足的属性/关系。比如，x>0 是一个约束，x>y 是一个约束，a∨b∨¬c也是一个约束。一个约束问题常常包含许多约束。

要做约束求解，首先得用数学语言来表达约束。约束模型，就是用来表达约束的数学语言。常见的约束模型包括

布尔可满足性问题（Boolean Satisfiability或Propositional Satisfiability, 简称SAT）;
数学规划（也称为运筹优化，尤其以混合整数线性规划为代表）;
可满足性模理论（Satisfiability Modulo Theories, 简称SMT），SMT其实就是限定背景理论的一阶谓词逻辑;
约束满足问题（Constraint Satisfaction Problem, CSP），这是一个普适的模型，以上其他模型都可以说是CSP的一种形式。

约束模型本质就是数学模型。还有很多数学模型，比如微分方程（包括偏微分方程PDE和常微分方程ODE），流体力学（Computational Fluid Dynamics，CFD），几何约束，等等，其实都是约束模型。不过，由于历史原因和学科原因，一般我们提到约束求解，大部分时候谈的是上面提到的几种模型及其变种，偏向于数理逻辑和数学规划，有时也包括几何约束。当人们谈及微分方程的时候，很自然会定位到微分方程这个具体的数学分支，而很少将其定位到约束求解。

每个约束模型也是一个数学问题。那么模型和问题怎么区分呢，为什么SAT问题就是一个模型，但是随便找一个组合优化问题就不会被认为是模型呢？一个问题要被称之为模型至少应该具备：

抽象性（数学化）
普适性（能表达某类不小的问题）
可求解（或者说在现实中大部分时候可以被求解，表达能力和求解性能的 balance）。

“求解”，顾名思义就是解决问题。对于以数学语言表达的约束问题，就是求出问题的答案。从这个角度讲，手算得到答案也是求解。但是一份算法伪代码不是求解。需要把算法进行编程实现，具体运行程序去算出问题的答案，才完成求解。

求解器，一般是指可以求解某个数学模型的程序。“求解器”也是一个广泛存在的概念，但不太为人所知。

先说一个大家都熟悉的东西，“计算器”，给定算术输入，比如1+1+4*6，则计算出结果=26。求解器可以看成超级计算器，做的事情本质上就是解方程。它的输入是方程（数学公式）。求解器面对的是各种形式的数学公式，可以是线性方程，比如“x+y=4, x-y=2” ，也可以是复杂的逻辑公式，比如这样，“(𝑥+y>10∨3x-z=2)∧(y=f(x+z)∨y-10z≥0)∧(𝑥+y+z=6∨𝑥≤4)”。这些输入我们一般称为约束，而如何求解这些约束的研究方向，就是“约束求解”，一个扎根于数学、结果于工业的方向，一个古老又仍然充满挑战的方向。求解器就是解决这些问题的计算机程序。

2.2 约束求解问题

约束求解问题，可以形式化表示为一个三元组的形式 P=<V, D, C>，其中的三个部分，含义分别为：

V：变量的集合，表示为{v1, v2, …, vn}；
D：变量的值域的集合，即每个变量的取值范围，即变量vi需要在其值域di内取值；
C：约束条件的集合，每个约束条件包含中一个或者多个变量，若 ci 中包含 k 个变量，则称该约束是这 k 个变量集合上的 k 元约束。

约束求解就是基于这一系列的约束问题，求出来一个解，这个解对所有的约束都满足，并且在自己的值域范围内，如果有这样的一个解，就说这个约束问题是可满足的，否则，就说这个约束问题是不可满足的。

当前，主流的约束求解器主要有两种理论模型：SAT求解器和SMT求解器。

2.3 SAT 问题求解

SAT问题（The Satisfiability Problem，可满足性问题），最典型的是布尔可满足性问题，是指求解由布尔变量集合组成的布尔表达式，是否存在一组布尔变量的值，使得该布尔表达式为真。SAT问题，求解的变量的类型，只能是布尔类型，可以解决的问题为命题逻辑公式问题，为了求解SAT问题，需要将SAT问题转换为CNF形式的公式。

下面简单介绍一些在SAT求解问题中的一些关键概念。

布尔变量（Boolean Variable）：即取值只能为真或者假的变量，布尔变量是布尔逻辑的基础（类似于Java中boolean类型的变量）。
布尔操作（Boolean Operation）：可以对布尔变量进行的操作，例如布尔与∧（类似于Java中 && 操作），布尔或∨ （类似于Java中 || 操作）和布尔非 ¬（类似于Java中变量前的 ! 操作）；
布尔表达式（Boolean Expression）：通过布尔运算符将布尔变量连接起来的表达式。如针对布尔变量a和b的布尔表达式可以是 a∧b（类似于Java中 a && b 操作），a∨b（类似于Java中 a || b 操作），¬a（类似于Java中 !a 操作），我们通过对这些简单的表达式不断进行或且非操作就可以变成很复杂的表达式，例如 (¬a∨b)∧(a∨¬b)（类似于Java中 (!a || b) && (a || !b)）。
析取(Disjunctive)：即布尔或操作。仅由布尔或运算符连接而成的布尔表达式为析取子句 (Disjunctive clause)。
合取(Conjunctive) 即布尔与操作。仅有与运算符连接而成的布尔表达式为合取子句 (Conjunctive clause)。

对上面的概念介绍完成后，我们可以给出CNF的概念。

合取范式(Conjunctive Normal Form)，合取范式，是命题逻辑公式的标准形式，它由一系列析取子句用合取操作连接而来。与之相反，析取范式 (Disjunctive Normal Form) 是命题公式的另一个标准型，它由一系列合取子句用析取操作连接而来。

如下： a∧(¬a∨b)∧(a∨¬b)：即为一个合取范式，最外层所有的连接都是合取操作；

a∨(¬a∧b)∨(a∧¬b)：即为一个析取范式，最外层所有的连接都是析取操作。

在传统的SAT求解器中，都需要提供一个CNF文件描述命题逻辑，扩展名是dimacs，然后将所有的变量和约束都定义到CNF文件中。

2.4 SMT 问题求解

如上面的分析，SAT求解器只能解决命题逻辑公式问题，而当前有很多实际应用的问题，并不能直接转换为SAT问题来进行求解。因此后来提出来SMT理论。

SMT（Satisfiability Module Theories，可满足性模理论），是在SAT问题的基础上扩展而来的，SMT求解器的求解范围从命题逻辑公式扩展为可以解决一阶逻辑所表达的公式。SMT包含很多的求解方法，通过组合这些方法，可以解决很多问题。

当前，已经有大量的SMT求解器，例如微软研究院研发的Z3求解器、麻省理工学院研发的STP求解器等，并且SMT包含很多理论，例如Z3求解器就支持空理论、线性计算、非线性计算、位向量、数组等理论。

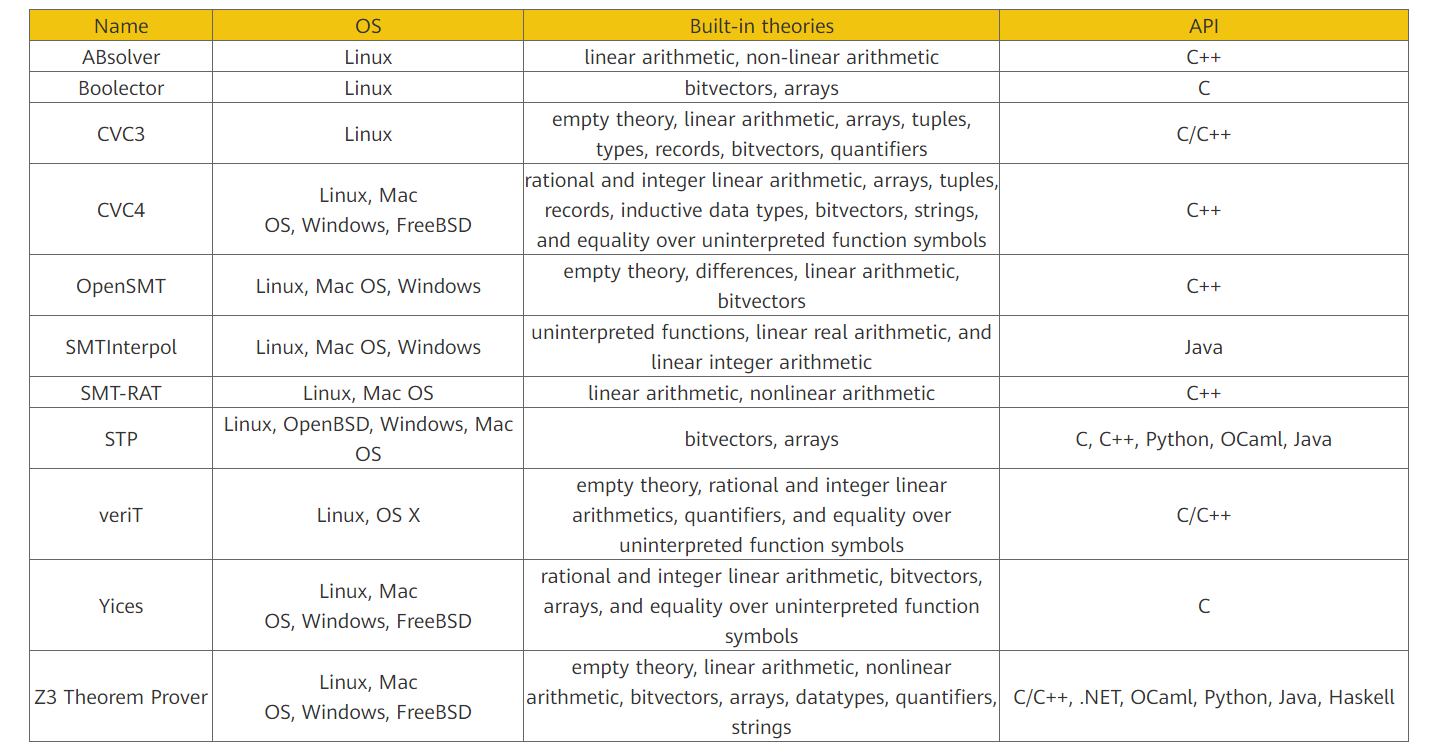
下面列举几种比较常见的SMT求解器（支持C/C++、Java、Python等主流编程语言的API）：

参考

公众号：Flowlet

「如果这篇文章对你有用,请随意打赏」